Line-Based Multi-Label Energy Optimization for Fisheye Image Rectification and Calibration
Mi Zhang, Jian Yao*, Menghan Xia, Yi Zhang, Kai Li and Yaping Liu
School of Remote Sensing and Information Engineering, Wuhan University, Wuhan, Hubei, P.R.China
*EMail: jian.yao@whu.edu.cn
*Web: http://www.scholat.com/jianyao http://cvrs.whu.edu.cn
[ ] The test dataset is added.download (8/4/2015).
] The test dataset is added.download (8/4/2015).
1. Abstract
Fisheye image rectification and the intrinsic parameters estimation for real scene have been addressed in the literature by using line information on the distorted image. In this paper, we propose an easy implemented fisheye image rectification algorithm with line constrains in the undistorted perspective image plane. We propose a novel Multi-Label Energy Optimization (MLEO) method for detecting and selecting long arcs from line images, from which we can obtain intrinsic parameters of fisheye camera utilizing only three circular arcs. The rectification and calibration framework are presented and long arc detection and selection algorithm have been implemented and tested in simulated and real image. We compare the results on real images with the approaches based on the circular arc detection and evaluate the performance of the algorithm for synthetic method.
2. Our Approach
Given a set of clustered circular arcs, our goal is to rectify the fisheye image and extract the intrinsic parameters from selected circular arcs. Our approach involves three steps: automatic circular arcs extraction from fisheye image, the image rectification using clustered circular arcs and the intrinsic parameters estimation using selected conics. In our framework, circular arcs are automatically extracted and selected by modelling the problem as a Multi-Label Energy Optimization (MLEO) issue. The clustered circular arcs are then served as the input for fisheye image rectification, resulting in a corrected image on perspective plane. Meanwhile, three candidate circular arcs which are used for intrinsic parameters estimation can be selected in the similar manner. In the selection process, we take not only the circular arcs information on fisheye image plane but also the property of corresponding lines on perspective plane into consideration.
The details of algorithm are described in the paper.
3. Supplementary Experiments
Apart from the experimental results illustrated in the paper and supplementary material, we will focus on the robustness and accuracy as well as comparison with some existed intrinsic parameters estimation approaches for fisheye image.
3.1. Accuracy and Robustness w.r.t. Noise
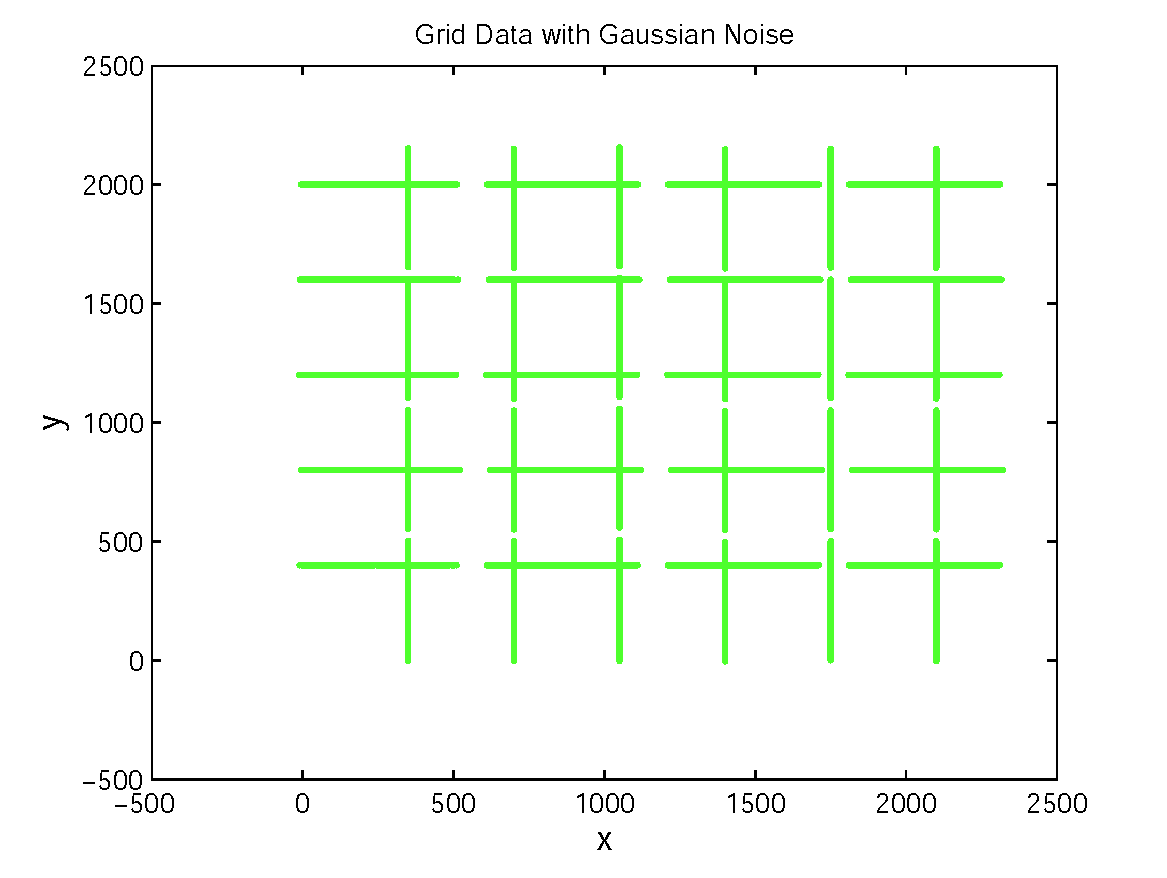
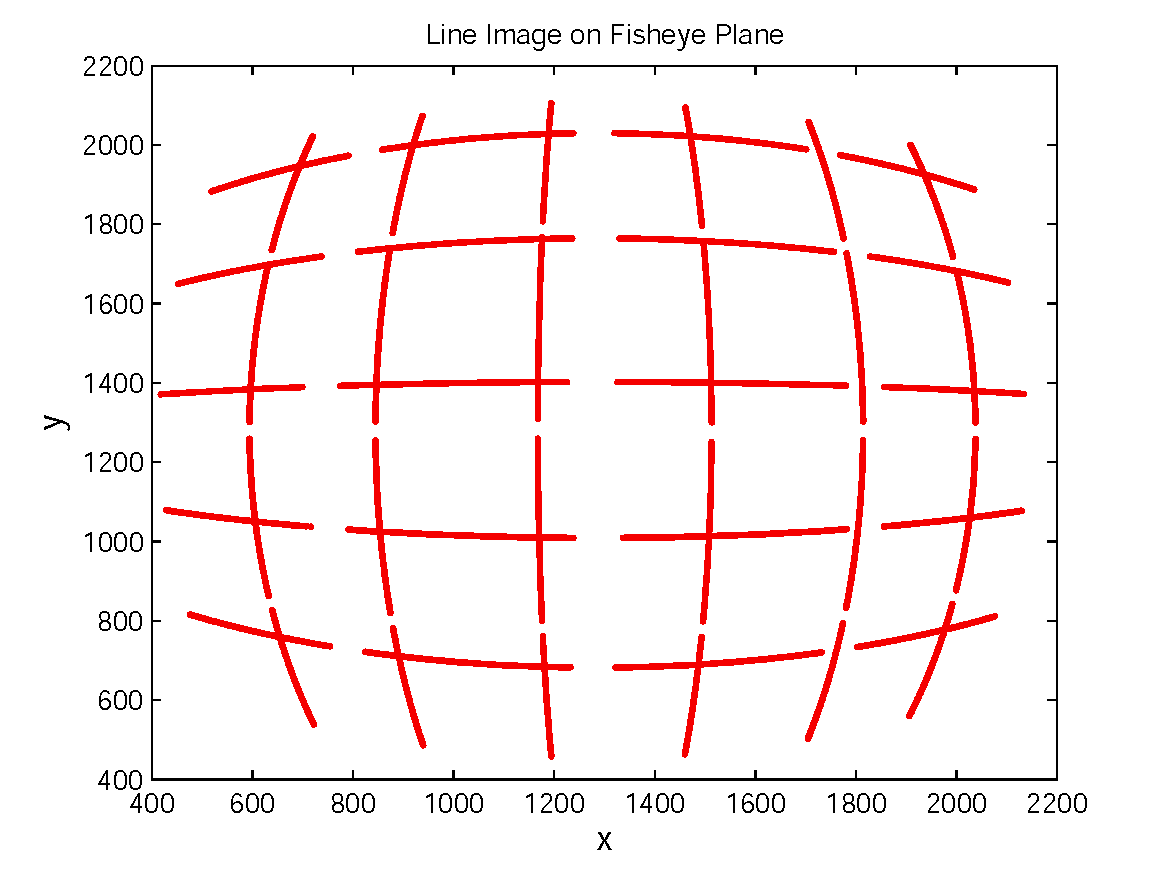
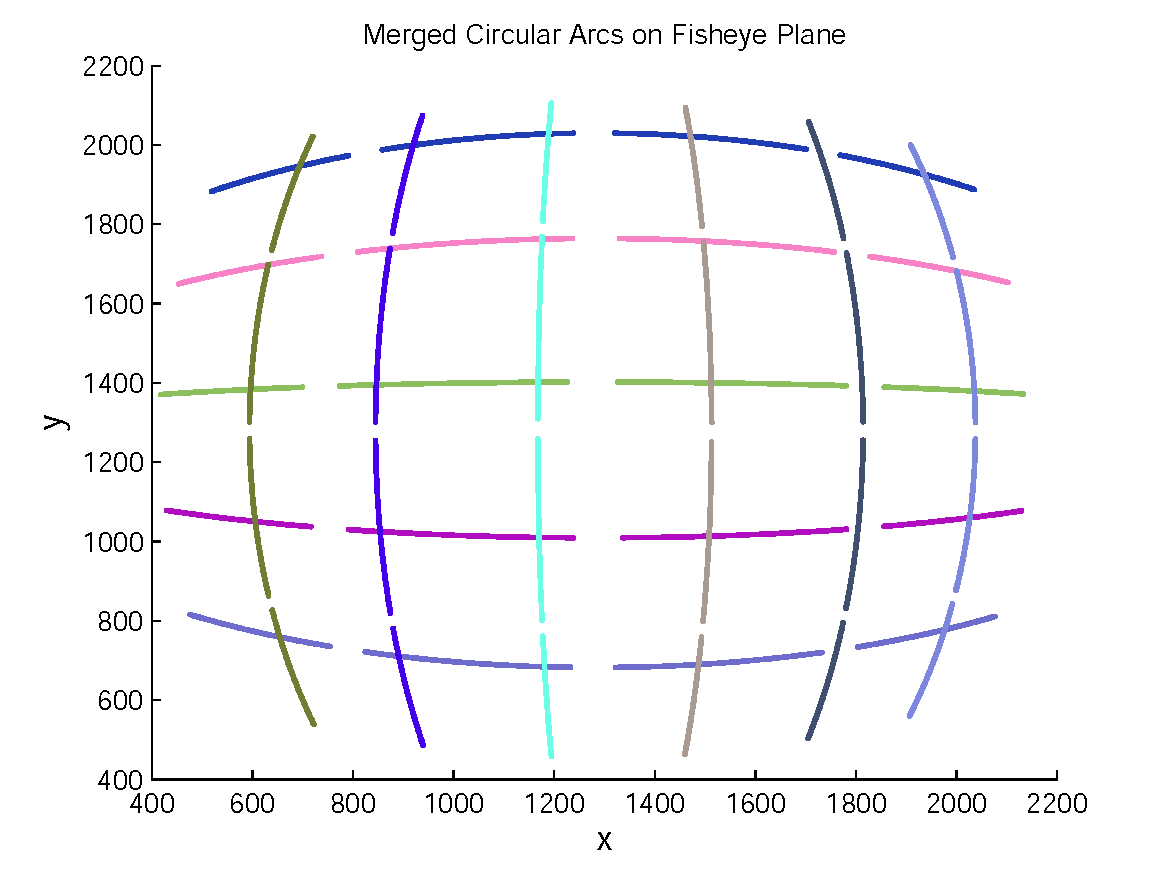
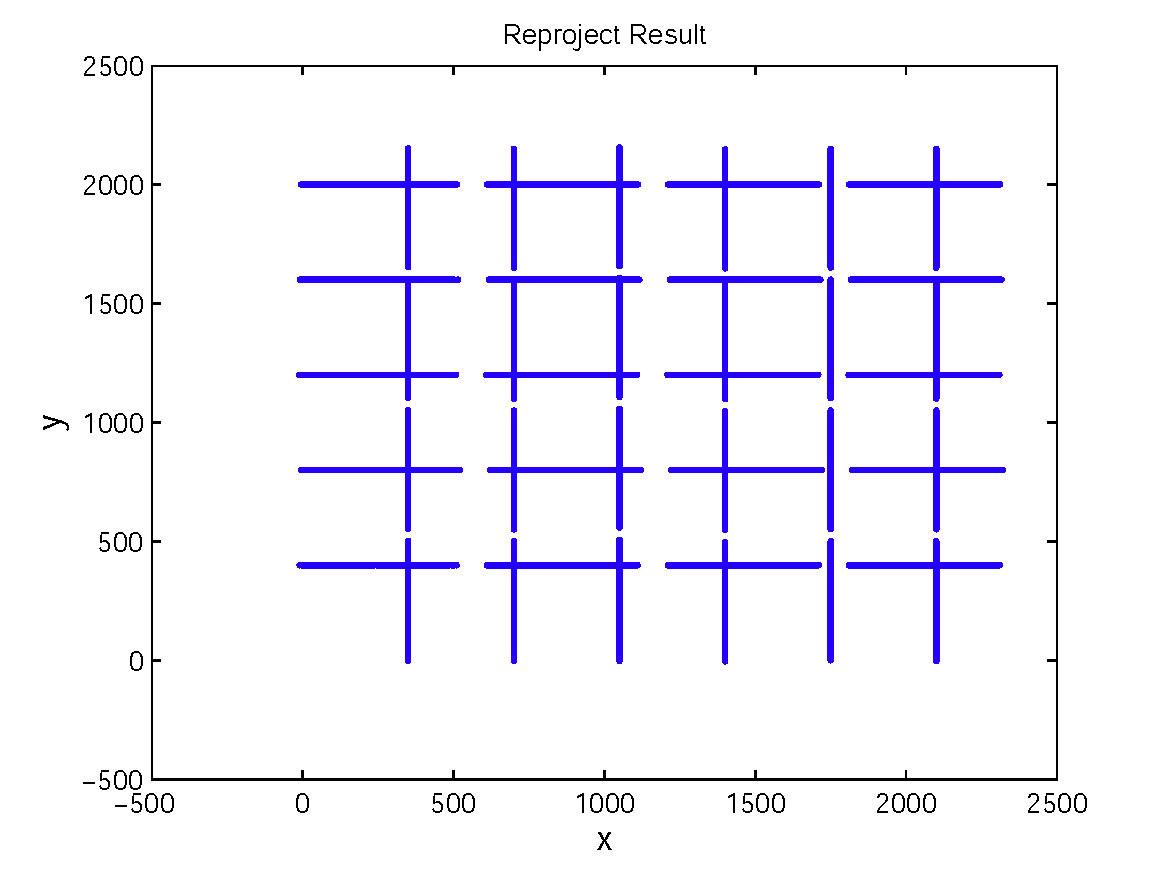
To demonstrate the accuracy and robustness of our method with respect to noise, we simulated the grid data consisting of 5 horizontal and 6 vertical lines. Each line is split into 4 segments (Figure 1(a)). After adding Gaussian noise, we transform the line segments to fisheye plane by Eq.(10) and estimate the parameters by Eq.(12). Finally, we project them to perspective plane (Figure 1(c)) and computed RMS w.r.t. ground truth data (line without noise). Figure 1(d) depicts the cluster result using our proposed algorithm, the segments belonging to the same circular arcs are correctly clustered. Experimental results shown in Figure 1(e) depicts that RMS become more and more stable w.r.t. noise for our approach.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
| (e) |
Figure 1. Accuracy and robustness with respect to noise: (a)Simulated grid data with Gaussian noise; (b)Correspond line segments on fisheye image plane; (c)Clustered line segments using our method; (d)Projected line segments by Eq.(9); (e)Computed RMS w.r.t Gaussian noise.
3.2. Comparative Experiments
In the Figure 2 and Table 1, we illustrate the intrinsic parameters estimation results using our proposed algorithm and the existing method with chessboard and CatPack (see the link in our paper). Figure 2 depicts the images captured by the same camera and the estimated circular arcs using our method and Catpack. Table 1 further demonstrate the estimated intrinsic parameters. It can be seen from Table 1 that the deviation of focal length from ground truth for our method is much smaller, which is important to maintain the characteristic for recovering the depth map in Structure From Motion (SFM) application.
 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
|
|
Figure 2. Intrinsic estimation for the same fisheye camera: (a)Source fisheye image for intrinsic parameters estimation; (b)Our selected circular arcs for intrinsic estimation; (c)Chessboard image captured by the same camera for intrinsic estimation; (d)Manually selected circular arcs for intrinsic estimation using CatPack.
| focal length | u0 | v0 | aspect ratio | |
| Ground Truth | 3200.000 | 3000.000 | 2000.000 | 0.000 |
| Ours | 3133.094 | 3034.289 | 2200.395 | 5.260e-11 |
| Chessboard | 3576.629 | 3025.500 | 2015.060 | 0.000 |
| CatPack | 2772.533 | 2568.431 | 1439.264 | 0.034 |
4. Additional Experimental Results
To further validate the performance of our approach, we tested the fisheye image downloading from Internet which consist of the indoor scene and outdoor scene. All these images are captured with different posture, illumination and exposure.
The results are showed in Figure 3, Figure 4 and Figure 5.


































